Here's the weird thing - when you look at thousands of galaxies, you see pretty much one type of motion - and that is motion away from us. It looks like pretty much every distant galaxy out there is moving away from us! All of their spectra show large redshifts (remember, velocity away from an observer shifts the spectral features to longer, or redder, wavelengths). Now not every single galaxy has a redshifted spectrum, but the number of blueshifted spectra seen in galaxies is pretty sparse, and that is mainly for galaxies that are near us. Apart from these few galaxies, pretty much all the others are moving away from us.
Now this is a really bizarre thing - but what does it mean, and what does it tell us about galaxies and the Universe? Just measuring the spectra and getting the velocities is only one part of the answer. It took some careful detective work to find the other piece of information to figure out what was going on, and that piece of information had to do with the distances of the galaxies. One fellow noticed that there was actually a trend in the velocity values with the distance values. That fellow was Edwin Hubble; you remember him, the guy who figured out that galaxies were separate, distant objects. He used his methods of obtaining distances to galaxies (by using Standard Candles) and combined that information with velocity data (obtained from the spectra of galaxies). Just how did he combine that data? - in a graph, of course.
If you plot up this data, you find that the greater the distance a galaxy is from us, the faster it is moving away from us. Put another way, distant galaxies are receding from us at great speeds. The greater the distance, the greater the speed away from us. This diagram, which was first constructed by Edwin Hubble is known, surprisingly, as a Hubble Diagram.
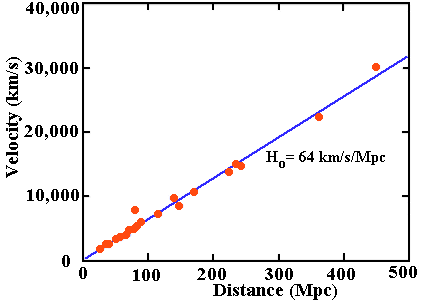Figure 1. A Hubble Diagram, simply a plot of galaxy
velocity versus galaxy distance. This diagram is based upon distances
found using Supernovae. The slope of the line gives the value for the
Hubble Constant, Ho. Data from Riess, Press and Kirshner (1996).
Now this diagram will only work on distant galaxies - nearby galaxies don't show this sort of trend since they are moving randomly around in their clusters - sometimes toward and sometimes away from us. For distant galaxies there is a direct correlation between the speed a galaxy is moving away from us and how far away it is from us. There must be a formula that relates these two things, distance and velocity. Of course there is! The data appear to fall along a straight line that can be drawn through the data, so the line represents the slope of the formula, and it can relate the two quantities. Guess what we call this formula? You guessed it; it's known as the Hubble Law.
Mathematically, the formula is written out as
v = Hod
where, v=velocity (in km/s), d=distance (in Mpc), and Ho is
the slope of the formula and appears to be a constant, which we'll call
the Goober constant - no, that's silly, we better stick with the trend
here and call it the Hubble constant (its units are km/s/Mpc).
This is a pretty simple formula, eh?
Not only is this formula pretty simple, but is probably one of the most important formulas ever written. THIS IS REALLY, REALLY GREAT!!!! Why? There are three reasons.
1. If you remember the discussion of Standard Candles, you know that there are some problems in finding accurate distances. The Hubble Law provides astronomers with another method for finding distances - so long as you know what the value of Ho is. How do we get Ho? You need data from galaxies, in particular their distances and velocities. Just take this data and plot it up like Hubble did, draw a line through it and you'll get a value for the Hubble Constant, since it is equal to the slope of the line. That sounds easy; get velocities and distances of galaxies so we can use the Hubble Law to find distances to galaxies. Wait a minute, if we want to use the Hubble Law to determine distances, we need to first have distances to determine what Ho is before we can use it to find distances - that's silly. This doesn't make sense. How can we find distances with the Hubble Law if we first need to have distances to get the constant? That's sort of the problem with the whole thing.
Astronomers can try many times to determine the value of the Hubble Constant using distances measured with Standard Candles and velocities obtained from galaxy spectra, but they rarely get the same value for the constant. This has been one of the biggest problems in astronomy since Hubble first did this in 1929. Each time someone tries to determine the value of the Hubble constant, they get a value that doesn't agree with anyone else's value, so there has usually not been much agreement on what value to use for the Hubble Constant. One of the reasons that astronomers don't agree with one another about the value for the Hubble Constant is that they use different methods or assumptions in getting distances, so they will get different values for Ho. Astronomers who do this experiment over and over even change their own ideas as to what the value of Ho is.
That's just dandy; how are we supposed to know what the value of the Hubble Constant is? Actually, things have gotten better since around 1999. Astronomers using the Hubble Telescope (which was not built by Edwin Hubble, it was just named for him) were able to measure distances using Cepheids and Supernovae in distant galaxies. Actually, several different groups of astronomers were doing this, so of course they ended up with slightly different values of the Hubble Constant. However when you look at all of the data it tends to converge to a value of around 70 km/s/Mpc. This is actually pretty good; it used to be that the values for the Hubble Constant that people calculated were widely divergent by large amounts. Typically, if you wanted to use the Hubble Law to get distances, you would pick a reasonable value based upon a project that measures it accurately, usually something between 65 and 75 km/s/Mpc. While the actual, precise value of the Hubble constant will never be known, if you used a value such as 70 km/s/Mpc, you wouldn't upset too many people.
It is sort of a good thing that the Hubble Telescope was able to do what it was built for, namely to help figure out what the value for the Hubble Constant is fairly accurately. Now it's onto another reason why the Hubble Law is so cool.
2. What exactly is Ho? What does it represent? According to the Hubble Law, Ho=Velocity/Distance. So what is Velocity dependent upon? It is basically Distance/Time. Therefore Ho = (Distance/Time)/Distance = 1/Time. It is related to a time. What does this time represent? The time value which Ho represents is the time it took for the Universe to expand to its current size, or another way of saying it is that it is a rough estimate for the age of the Universe - good gravy, that's one of those basic questions of life, the universe and everything. That's sort of an important number - not as important as your student ID number or your weight, but it is one of those numbers that have been on people's minds for a long time.
3. The last reason why the Hubble Law is so valuable is why it even exists at all. That's a rather interesting thing - why does it exist? Why are those more distant galaxies moving away from us at greater velocities? The Hubble Law exists because of what the Universe is doing - it is Expanding! If the Universe weren't expanding or moving in some way, there would be no trend in the velocities. Hubble wouldn't have been able to make that nifty plot of his if the Universe were sitting still. We'll look at this aspect more closely later.
The Hubble Constant is a pretty important thing. Why can't we figure out what its value is simply? It is easy, isn't it? No, it is not easy at all, but is a rather complex step-by-step process. There are many places to mess up in the process.
To determine the scale of the Universe, you must first start closer at home. You need to determine the distance to the Sun, the AU. Why? The concept of parallax is based upon our orbit about the Sun, so the size of a parsec depends upon the size of the AU. Once we know how big an AU is, you can start to find the distances to nearby stars (using the parallax method), then the distances to more distant stars (using the properties of the nearby stars and methods such as spectroscopic parallax), then the distances to nearby galaxies (using various Standard Candles, which are based upon the characteristics of those stars that you looked at previously in your own galaxy), then the distances to more distant galaxies (using the characteristics of the nearby galaxies) and so on.
As you go further out, more assumptions, more uncertainties, more inconsistencies between various scientists, more guess work, and more shaky ground pops up. No wonder those silly astronomers can't agree; it's too much of a mess to begin with!!!!
Two things that we like to measure with stars are mass and luminosity, and this is also true with galaxies. Let's see how that is done, shall we? Unfortunately, with galaxies being so far away, it isn't always possible to determine their masses accurately. There are a few special situations where the mass can be determined, though, and these are done by using methods you've already seen before - by looking at how quickly a galaxy rotates and by looking at the motion of binary galaxies.
The first method, using the rotation of the galaxy, is the same way that we determine the mass of the Milky Way. If you measure the speed of rotation (from the galaxy's spectrum) of a distant part of a galaxy, you can then use Kepler's laws to figure out how much mass is located within the orbit of that distant part. There are a few problems with this method, mainly that it really only works well for spiral galaxies, so it can't be used for all types of galaxies. You also want to have the galaxy tilted so that the velocity is directly toward/away from us. If the galaxy is tilted at a random angle relative to our view, we have to take that into account when figuring out the velocity and therefore the mass of the galaxy, so it is always better to have direct motion toward or away from us. We also have to take into account the overall velocity of the galaxy through space. Once we do that we see that spiral galaxies rotate pretty much like the Milky Way does - and this supports our observations of our own galaxy.
Figure 2. Several
galaxies in a group. The motions of these galaxies about one another
can help determine their masses. Image Credit: Hubble Heritage Team
(STScI/AURA/NASA).
The other method used to figure out the mass of a galaxy is to observe a binary galaxy system. This is just like using binary stars to determine the masses of stars. There is only one small problem. Galaxies are like giant lumbering elephants - they don't appear to move very fast as we see them. This is in part due to their great distances. If a jet plane were 30 feet from you and it went by it would obviously look like it was moving fast, but when it is 30,000 feet up it appears to be just inching along. It isn't actually going at a slower speed, but the apparent distance it covers looks to be less since it is further away from you. Now extend this to galaxies. These beasts can be moving at hundreds of kilometers per second around each other, but because they are so far away you never see any visible motion in your lifetime. Even if you live to be 100 years old, you won't see any motion. Even though we can't see the motion, we can still get a clue as to how fast they are moving based upon how their spectra are screwed up by the Doppler effect. There is a problem with this. The Doppler effect only measures velocities toward or away from you, not velocities that are side-ways. No matter how long you look or how carefully you analyze the spectra, you'll never accurately measure the entire velocity of a pair of binary galaxies. Often astronomers have to guess about the amount of velocity they are missing. I suppose I should not say guess, since that sounds like we're throwing darts at a board and using those numbers. We really don't do that, but instead use various statistics to figure out how much of the velocity we are missing.
Any ways, after we estimate the velocities and the separation of the
binary galaxies, we can get their masses using Kepler's Third law, just
like with binary stars -
M1+M2 = a3/P2
where M1 and M2 are the masses of the galaxies and a
and P have their usual meaning. As with binary stars, the masses
are in solar masses, the distance is in A.U.s and the period is in
years. Isn't that nifty? Kepler's simple little law works for more than
just planets; it works for whole galaxies!!! You probably didn't think
I'd get this much mileage out of that one silly little law did you?
Actually, you could even use this method to get not only the mass of
two galaxies going about one another, but of a whole bunch of galaxies
going about each other. All of their masses are influences on one
another, so they would all feel one another's pulls and would all obey
Kepler's Third law, but in this case one of the M values in the formula
is the mass of the whole group of galaxies.
Figuring out the luminosity of a galaxy is pretty tricky, since sometimes it is difficult to figure out where the end of a galaxy is. Longer and longer exposure pictures of galaxies (spiral galaxies especially) show larger and larger sizes and more and more stuff. Just where does a galaxy end? At some point astronomers have to say enough is enough; we'll only measure out to a certain distance and add up all the light to this distance. Then the guessing game is played again - how much light are they missing by not seeing the stuff beyond this point? How much light are they missing that is covered up by dust and gas within our galaxy or by the dust and gas within the galaxy they are looking at? What about the light sources that produce only IR or UV light? There are quite a few fudge-factors that come into play in luminosity estimates for galaxies because of the limitations we run into. Typically, we measure galaxy luminosities in terms of the Sun's luminosity.
In spite of all of these problems, once the mass of a galaxy is known, it can be compared to the luminosity of the galaxy. Why? You know that astronomers like to do weird things with numbers. Actually, we just don't compare these numbers; we divide them. This gives us the M/L ratio - Mass to Luminosity ratio. This is sort of an important thing. What if galaxies are made up of average stars that are like the Sun? If that were the case, you'd expect to measure the same amount of mass as you would luminosity from the galaxy, so the M/L value should be close to one. What if a galaxy is ultra luminous or abnormally bright for the amount of mass contained within it? If that were the case, there will be a large L value compared to the M value, so M/L would be low (much less than one). The third possibility is if there is a ton of material but it is really dark and not giving off much light, so there would be a huge amount of M but not so much L, and then we would have a large M/L value (much larger than one).
That's all fine and dandy, but what do we see for the M/L values of galaxies? For spirals, the M/L value is about 35, and for ellipticals, the M/L is about 70! What does this mean? It tells us that there is a great deal of dim stuff in galaxies - it makes up a lot of mass but doesn't show up in our telescopes (doesn't produce much light). This means we are missing out on seeing a lot of the stuff that is out there. Remember, the only way we can see stuff is if it produces light, and with such high M/L values, we know that we are missing a lot of stuff.
It is sort of hard to determine the distribution of the different types of galaxies, such as determining how many ellipticals, spirals, and irregulars there are. The problem is that at great distances, the really small galaxies would escape detection. Even if there were many small galaxies (like dwarf ellipticals, dwarf spheroidals or small irregulars), we would have a hard time seeing all of them. Some astronomers say there are more irregulars, while others believe that there are more ellipticals (especially the dwarf ellipticals and spheroidals). We'll need more information before we can settle this debate. Where have I heard that phrase before?
You've seen that there is quite a wide variety of galaxy types and that the content, sizes, shapes and masses of galaxies are very diverse. Is there any link between the various types? For example, if a galaxy observed today is an SBc, will it always be an SBc or can it change into an Sc, SBb, or whatever? How does a galaxy end up being a spiral, an elliptical or an irregular? What determines these things? Why is it that someone always calls you just when you're ready to sit down to eat dinner? Oh, I guess this last question really has nothing to do with galaxies.
Let's tackle the easiest parts first. We know that ellipticals have sort of spherical blobby shapes and no new star formation in them. This means that they made their stars very early in their lives and then that was it - no more star formation - sort of a like a kid who eats all of their Halloween candy at one time. They end up rather blobby and spherical. Spiral galaxies, on the other hand, are still making stars, so they didn't use up all their gas when they formed. They are like the kid that slowly rationed out the candy, eating only a little at a time so that it lasts longer. Why would they do either of these things - using up all their gas or rationing it out? What could be the reason for different galaxies to act in different ways?
One of the simplest explanations is to look at how a galaxy moves. An elliptical galaxy has all of the material moving in a swarm about the center, while a spiral has a well organized disk that is rotating. Why are they different? One of the reasons that things may move the ways they do is angular momentum. You'll remember this was the thing that makes the ice skater spin faster when the arms are brought in. Angular momentum also has some say in how things will move and how fast they will move. If an object, like pizza dough, is spinning really fast, it will tend to flatten out in a disk as gravity pulls the material in. It is thought that this is what was happening with spirals, that they were spinning pretty fast when they formed, so that the gas didn't all blob together in the middle but got spread out into a disk. If the gas is spread out it isn't going to go into making stars immediately (remember, you have to compress it to a certain degree). Elliptical galaxies, on the other hand, may have originally been slow spinners, so they didn't flatten out, and the gas just globbed together quickly (due to gravity) and formed all the stars right away. If this idea about how they rotate is correct, then we would expect to see more elliptical galaxies forming before spirals forming, since the ellipticals' star formation isn't delayed. We do actually see this. At great distances we see many well formed elliptical galaxies but very few fully formed spirals - they are taking their sweet time to form. As we'll see later, having ellipticals form quickly can have some interesting consequences, especially when it comes to their cores (or more precisely, what forms in their cores - but I don't want to give that away).
Let's get to some specifics of the life cycle of a spiral. It is now thought that spiral galaxies can change quite a bit over their lives by having bars form in them and then having these bars dissipate over time. The bar can redistribute the material in the disk and the bulge over time and alter the rate of star formation, the chemical composition and the galaxy type. Other things can also alter the shape of a spiral, such as having another galaxy get a little too close to it and re-arrange the material. It is possible for a galaxy to form as a type Sc, become an SBc, then an SBb, then an Sb and then an Sa through various processes. Of course, these changes will take millions or billions of years to occur, but they can happen nonetheless. At this time is not entirely clear how the shape of a galaxy will change over time since both internal and external factors can play a role.
Figure 3. Click on this icon to see several
examples of how a galaxy can change. The rate at which it collapses,
interactions with other objects or the influence of a bar can all play
a role in altering the shape or content of a galaxy.
Irregular galaxies tend to be produced by collisions or near-collisions of galaxies. The strong gravitational pull of big galaxies on little galaxies can cause the material in the little galaxies to be completely stripped off or re-arranged in a bizarre shape. There are also cases where the little galaxy can screw up the big galaxy - no one is immune from the forces of gravity; it just depends upon how things come together and mess up one another. Our own galaxy is going to collide with the Andromeda galaxy in about two billion years. A simulation showing how that may look to someone located far away is provided here (animation visualization by Frank Summers (Space Telescope Science Institute). Simulation by Chris Mihos (Case Western Reserve University) and Lars Hernquist (Harvard University). Since this collision will start before the Sun dies, it could result in our solar system being flung out of the galaxy. When the collision finally finishes (in about 5 billion years) and everything settles down, the Sun (and the planets) could be located far from the center of the newly merged galaxy, possibly in the outer halo of the newly formed galaxy. Or it could be found amongst the other stars in the newly merged elliptical galaxy. Either way, it's something we can look forward to.
Figure 4. An
image of a group of galaxies known as Stephan's Quintet. These galaxies
are interacting with one another. If you click here,
you can see a computer simulation showing how these galaxies are
possibly moving and interacting. Image credit: N.A.Sharp/NOAO/AURA/NSF.
Animation credit: Credit: Joshua Barnes (University of Hawaii).
The giant elliptical galaxies (cD types) are thought to be produced by cannibalism, and this idea tends to gain favor because there are often remains of the "victim" galaxies still visible in the cores of the cD galaxies. When you look at the locations of cD galaxies in groups of other galaxies, they tend to be right in the middle, just like a big, fat spider in the middle of a web. It doesn't necessarily mean that the cD galaxy will eat up all of its neighbor galaxies, but if something does get too close, it better watch out.
Once people realized galaxies are objects outside of our own galaxy, they noticed that galaxies are not randomly scattered across the Universe. They tend to be found in groups or clusters - what an original name!
Figure 5. A
typical galaxy cluster, in this case the Virgo cluster. This one is
rather large having a few thousand galaxies in it. Only the brightest
are visible here. Image courtesy of NOAO/AURA/NSF.
Our own galaxy is in such a cluster known as the Local Group. This contains around 70 galaxies with the big ones being our own Milky Way, the Andromeda Galaxy (M31), and the Triangulum Galaxy (M33). There are many smaller galaxies including the Large and Small Magellanic Clouds, the little ellipticals that hang around Andromeda and a bunch of others. Actually, the little galaxies (irregulars and dwarf ellipticals) outnumber the big galaxies by a wide margin. The extent (diameter) of our cluster is only around 1 million pc. It is such a pain to write out all of those zeros that we'll just define a new unit of measure called the Megaparsec (Mpc), which is a million parsecs. There is also the unit of a Megalightyear, which is obviously a million lightyears. These two units are often used to describe distances to galaxies or the sizes of galaxy clusters.
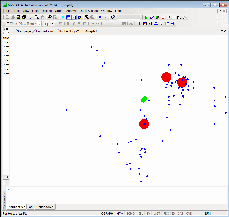Figure 6. The Local Group seen in three dimensions.
If you click on the image you can see how the members of the Local
Group are spread out. The Milky Way is the large red dot in the center, while
the other two major galaxies, Andromeda and Triangulum, are the other two
red dots. The Large and Small Magellanic clouds are the green dots. All of
the other dots are dwarf elliptical, spheroidal or irregular galaxies. Sizes
of galaxies are not to scale.
While you might think that the Local Group is pretty good sized, there are actually other clusters that are larger, and I mean much larger. Some clusters have a great number of galaxies and cover a correspondingly larger span of the Universe than our little Local Group. Clusters can contain thousands of galaxies spread over dozens of Mpcs. Generally, clusters are distinguished mainly by their size. Those with a lot of galaxies are termed as Rich, while those with few galaxies are known as Poor.
Figure 7. The Coma Cluster of galaxies. This picture
shows hundreds of galaxies. Nearly every object in this picture is a
galaxy - only a few of the objects are stars located in our own galaxy.
This is clearly a rich cluster. Image credit: Omar Lopez-Cruz & Ian
Shelton/NOAO/AURA/NSF.
Clusters are the way they are because of gravity. One of the effects of gravity is to bring some of the galaxies into close proximity, which can lead to galaxy collisions or mergers. Astronomers find that there are many collisions going on, or have gone on in the past. In some clusters collisions can be on-going or happen every few billion years. In the end the galaxies in the cluster could all merge into one large central galaxy - usually an elliptical. But that would take a very long time. You can see a simulation of a galaxy cluster's motion here - this simulation spans nearly the entire history of the Universe, around 14 billion years.
Based upon the ages of stars in them, we know that galaxies have been around for billions of years and they are moving around in clusters at pretty good speeds, yet the clusters stay together - the galaxies don't generally drift or fly away. They are gravitationally bound systems - the galaxies are orbiting about one another and stay together due to their mutual gravitational attraction. If we can determine how fast the galaxies are going then we can figure out how much mass is needed to keep them in a group - how much gravity is needed to counteract their outward velocity. This is another way of measuring the masses of galaxies, or even the masses of a whole group of galaxies at once.
If you remember back to the discussion of galaxy masses and luminosities, it seemed that we always detected more mass than light from galaxies. Is this the result we get when we look at a whole bunch of galaxies? Yes! When we look at whole clusters of galaxies, we tend to see much less material than there needs to be to hold the group together, or putting it another way, there is a very high M/L ratio. I'm really getting sick of this high M/L thing - why do we always detect more mass than we can see? Perhaps we're just using the wrong types of telescopes? Perhaps a lot of the matter in galaxies and clusters of galaxies is only visible at IR, UV or radio wavelengths? I'm sorry to say that's not the answer. We've tried to look for the material at these wavelengths and we still don't see enough stuff to account for all of the mass that is in the galaxy clusters or the individual galaxies. We just aren't seeing the stuff at all! Now things are going to get a little silly. It appears that a large fraction of the stuff in galaxies or even galaxy clusters is not visible to any telescope. We're basically saying that we have a hard time seeing most of the material that makes up even our own galaxy. What could this stuff be? This is that same sort of thing we saw with the Milky Way Galaxy, the presence of a large amount of unseen material. If you remember, we refer to this stuff as dark matter - sort of a cool name, don't you think? Dark matter comprises 90% or more of the total mass of a cluster of galaxies. That means when astronomers look at groups of galaxies, or even our own galaxy, they can only see 10% of the stuff that is in the galaxy or the galaxy cluster. We are not seeing most of the stuff! That is like someone who studies plants or flowers only being able to see one petal or leaf from the plant. We're really missing most of the stuff that is out there.
If most of the stuff that is out there is dark matter, what is it? What stuff can be so abundant, yet remain undetectable? There are two main ideas as to what type of stuff comprises the dark matter. One idea was put forth by people who do physics - there are a lot of funny little particles that exist in nature, like the neutrino, which are really hard to detect. Such particles are hard to detect because they don't interact with things very well, sort of like Patrick Swayze in "Ghost" - you don't know he is there most of the time unless you are Whoopi Goldberg, but even then you aren't detecting all of him. Neutrinos are like this - they don't interact with much stuff, so we don't know how many of them are out there. Now what would happen if a neutrino has mass, even just a little mass? There are so many neutrinos, you would have a bunch of mass that would not be visible! This is exactly what we are looking for - a particle that escapes detection, is very abundant, and has some mass. This is one of the possible forms that dark matter can take. We just can't call it a neutrino since it could be some other particle, so we have to give it a really cool name (mainly because we don't know what it really is) - WIMPs, which stands for Weakly Interacting Massive Particles. This could be just what we were looking for. The only problem with this idea is we don't know if these types of particles exist - remember, we can't detect them very well. It is possible that there are other things out there besides neutrinos which we can't detect at all, so we may never be able to say for sure if the WIMPs are the stuff that make up the dark matter.
If the WIMPs aren't the stuff that makes up the dark matter, then what is? Astronomers probably didn't like having the physics people come up with the answers to an astronomical problem, so they came up with MACHOs (not because astronomers are tough and physicists are wimps, or perhaps that is the reason...), which stands for Massive Compact Halo Objects. What does that mean? It means these are massive objects, but they are small in radius and they are found in the halos of galaxies. What sort of massive objects are these? We've already run across quite a few exotic, compact objects like black holes, neutron stars, and white dwarfs in our discussion of stars. There are also all those really ultra-faint L and T type stars that would be difficult to detect. What if there were tons of these little stars or lots of black holes out there? They would contain a large amount of mass in them, yet they would not be producing very much light. This is just we are looking for. Some astronomers are actually trying to find MACHOs out there. They do this by watching a whole bunch of stars - millions of stars each night. If a MACHO were to pass in front of one of these stars, the light from the star would be effected in a predictable manner. Now this sounds like a really boring thing to do - watch several million stars to see if any of them flicker, but that is exactly what is done. Various projects that are doing this have detected some MACHOs in the halo of our galaxy. We're still not sure if we're seeing as many MACHOs as we should so that they could account for all of the Dark Matter in our galaxy, but some of them have been found.
MACHOs are sort of the "normal" objects, while WIMPs are the "abnormal" objects that can make up Dark Matter. Which is it? Is the Dark Matter in the form of WIMPs or MACHOs? We have detected small amounts of both (remember, we can detect neutrinos from the Sun and supernovae), but we're still not sure of the numbers. It is possible that the Dark Matter is made up of various amounts of both WIMPs and MACHOs, though we're not sure of the amounts. There are many projects involved in the search for Dark Matter and here is a list of some of those projects. Even though we don't know if it is made of WIMPs or MACHOs we're still working on it, so I can't give you a definitive answer. Just give us a few more years and perhaps I'll be able to tell you something more substantial - or perhaps not - who knows?
After astronomers started grouping galaxies into clusters they noticed that on larger scales the clusters tended to be grouped together in clusters or what we call Superclusters (what a clever name - sounds almost like a superhero). Our cluster, the Local Cluster, is part of the Local Supercluster, which contains about 10 large (rich) clusters - our cluster is one of the many small clusters in it. Actually, in the old days the Local Supercluster was referred to as the Virgo Supercluster, mainly because the Virgo Cluster was one of the bigger parts of it. To get a sense of where we are, here is a 3-D display of various things in our neighborhood and beyond. You can zoom out to the Local Supercluster scale to see many of the galaxies "close" to us.
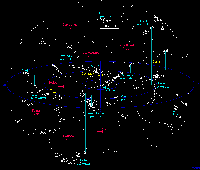Figure 8. A graph showing the locations of
superclusters around our own (we're in the middle). This map shows the
material within about 1 billion lightyears distance from us. Image is
from Richard
Powell's website.
If there are clusters of galaxies and clusters of clusters, are there clusters of Superclusters? This is getting silly, but it isn't a silly question, especially when you look out into space and see how the superclusters are arranged out there. It appears that there is a kind of structure to the Universe; things are not smoothly distributed. Clusters and superclusters tend to be grouped together. When we map out large areas of the sky and look at the distances and locations of galaxies, clusters of galaxies and superclusters of galaxies, we see some very large scale structure in our Universe. The image below is from a survey of the sky in two directions from the Earth. Notice how many bubbles and holes there are in the image - stuff is clumpy!
There are regions with very little matter (called voids) and other regions with large concentrations of galaxies (superclusters or even clusters of superclusters). Matter isn't evenly spread out but appears to be rather clumpy. This is an important characteristic of the Universe that we'll run into it later. There are many surveys that are mapping out this structure to our Universe (often refered to as Large Scale Structure) and the results from the various surveys are consistent - the Universe isn't smooth!
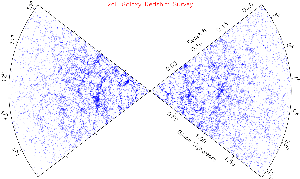Figure
9. A graph of around 220,000 galaxies
surveyed in two directions of the sky. The Earth is in the middle of
the wedges. Each dot represents a galaxy. To be precise, the sizes of
the dots are much too large (not to scale), so there is really not as
much crowding in the distribution of galaxies. With this in mind it is
obvious that the galaxies aren't uniformly spread out but clumped
together in superclusters or even larger scale features. There are also
many regions where there are no galaxies, which are very empty
stretches of space. Click on this image to get the larger version of
it. Picture is from the 2dF Galaxy Redshift Survey.