 Figure
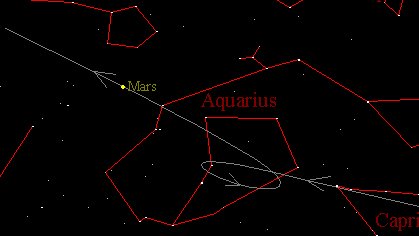
1. The path of Mars over several months has it moving slowly
eastward relative to the stars except for a few weeks when it moves
westward (to the right)
Figure
1. The path of Mars over several months has it moving slowly
eastward relative to the stars except for a few weeks when it moves
westward (to the right) How is science actually done? Do people just suddenly come up with ideas out of the blue, and we take those ideas to be truths? Generally no. Most often you hear about the Scientific Method which is the general method that describes how science is done, how discoveries are made, and how we can expand our current knowledge about how things work, all within a framework of "quality control". The scientific method can have several steps which are comprised of the following
Eventually a scientific hypothesis will pass the test of time, and have support through many observations or experiments such that it can be considered a theory. And just like a hypothesis, a theory can NOT be proven to be true, but it can be tested, supported, or refuted. Theories should be considered a "work in progress". Many theories exist in science, and those that you tend to learn about today are those that have passed the test of time, as well as many other tests and are accepted by scientists and society.
So if a theory lasts long enough and passes enough tests does it ever get placed into another category, such as "this is the truth"? No. Theories are always theories (unless they are shown to be wrong, in which case they tend to be ignored).
Along with theories, scientists have laws. The best way to think of laws is as a way of describing something. Laws can tell you how something will act or behave, but laws can not explain why something acts or behaves in a certain way. That's actually what a theory should do. Theories give us the "why", while laws give us the "how". One explains, the other describes.
While the Scientific Method may seem like a rather formal way of describing how science works, you have to remember that this isn't the way things were always done. In the past there may not have been testing or even an attempt to test a hypothesis. Sometimes ideas were just accepted without argument or discussion. Is that any way to do science? Today a scientist has to do several things before a new idea or concept is developed or becomes accepted
Perhaps the most complex motions that early astronomers had to deal with were those involving the planets. There are some rather complex motions that have to be explained and understood, since there was a great deal of importance placed upon planets for astrological reasons, though some cultures had some interest in planets for other reasons. For example, two planets, Venus and Mercury,were always seen near the Sun. Sometimes they were seen in the morning sky before the Sun rose, sometimes in the evening sky after the Sun set. Another annoying aspect of planetary motions was the way that the other planets (Mars, Jupiter and Saturn) would sometimes appear to stop in their motions relative to the stars, go backwards for a while, and then again go in their regular paths (eastward amongst the stars). These motions had to be not only explained but also predicted.
 Figure
1. The path of Mars over several months has it moving slowly
eastward relative to the stars except for a few weeks when it moves
westward (to the right)
Figure
1. The path of Mars over several months has it moving slowly
eastward relative to the stars except for a few weeks when it moves
westward (to the right)
In order for early astronomers to predict the motions of the
planets, they needed to make models of the sky which would explain its
workings. Unfortunately, most of these models made several bad
assumptions -
1. Geocentric - Earth is in the middle of everything. While this
may seem egotistical, there was also the idea that the Earth was not
moving, since you don't feel any motion. It was just easiest to put the
Earth in the middle. Later there were some philosophical and religious
reasons for putting the Earth in the middle.
2. The Sun, Moon, and planets have their own orbits about the Earth.
Obviously if the Earth isn't moving, everything else must be moving.
3. The stars are located on the Celestial Sphere. We already went over
this, and how the rotation of the sphere explained the motion of the
stars (though of course it's wrong, like everything else on this list).
4. All motions are along circular paths and at a steady rate. Another
way of saying this is that there were uniform
circular motions. Ancient astronomers were really hung up on the
idea that stuff in the sky had to move in paths that were perfect
circles, or associated with circular objects.
 Figure 2. An
ancient tablet with astronomical observations. The text of the tablet
is a copy, made at Nineveh (currently Iraq, but long ago Babylon) in
the seventh century BC, of observations of the planet Venus made in
the reign of Ammisaduqa, king of Babylon, about 1000 years earlier.
Image is from the British
Museum.
Figure 2. An
ancient tablet with astronomical observations. The text of the tablet
is a copy, made at Nineveh (currently Iraq, but long ago Babylon) in
the seventh century BC, of observations of the planet Venus made in
the reign of Ammisaduqa, king of Babylon, about 1000 years earlier.
Image is from the British
Museum.
The whole story starts with the Babylonians. They were amongst the
earliest astronomers who recorded the motion of the planets in the sky
and produced detailed star charts. They are the ones we have to
thank for the astrological signs and that whole business - though the
Egyptians did also contribute some of the ideas. By watching the motions
of the Sun and the Moon, the Babylonians were also able to predict
events such as eclipses. Their main contribution was their accurate and
long term recordings of the motions of objects in the sky. These
detailed records outlasted the Babylonians and were later picked up by
other civilizations. I guess they get the award for thorough record
keeping.

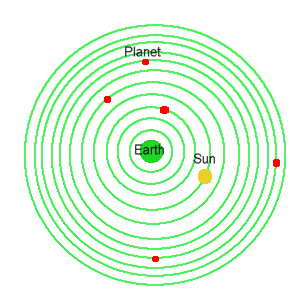 Figure 3. Aristotle's model of the sky, made up
of many concentric spheres, with the Earth in the middle
Figure 3. Aristotle's model of the sky, made up
of many concentric spheres, with the Earth in the middle
Another aspect of his model that was later used by other astronomers was that by having the Earth sitting fixed in the middle of the solar system there would be no stellar parallax. Parallax is the apparent shifting of objects caused by your changing direction of view. That explanation was as clear as mud, so let's try a little experiment. Take your thumb and hold it out at arm's length. Line it up with some distant object, viewing it with just one eye. Now switch your eyes (by this I mean close one and open the other). What happens? Did your thumb move? Didn't you hold it steady? You probably did, but you also did change the direction from which you were viewing your thumb. By viewing something from a different direction (or location), the alignment of things changes. This shifting is the parallax. See Figure 4 for what's happening. What does this have to do with the idea that the Earth is sitting fixed in the center of the solar system? What would happen if the Earth did move? Ancient astronomers thought that if the Earth was moving, it would be like shifting your eyes - at one time you would see a nearby star in front of one group of distant stars, and when the Earth moved to a different point in its orbit, you would see it in front of a different group of stars. This is just like the way that your thumb appeared to move when you changed your view. Ancient astronomers could not see any parallax motion of the stars (stellar parallax). They thought it was due to the fact that the Earth wasn't moving - no motion, no shift in perspective, no observed stellar parallax. Unfortunately, there is another explanation for the lack of observed parallax; can you think of it? The ancient guys didn't but we'll get to it later.
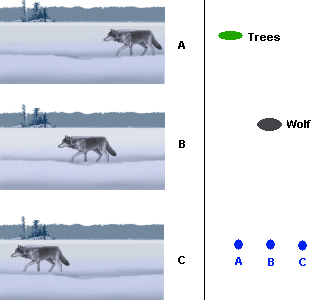 Figure 4.
Parallax demonstration. Each observer (A, B, C) sees a different
alignment of the wolf and the distant clump of trees. This type of
change in how the world looks based upon where you are located was one
of the reasons people did not believe the Earth moved (since they could
see no change in the relative positions of stars).
Figure 4.
Parallax demonstration. Each observer (A, B, C) sees a different
alignment of the wolf and the distant clump of trees. This type of
change in how the world looks based upon where you are located was one
of the reasons people did not believe the Earth moved (since they could
see no change in the relative positions of stars).

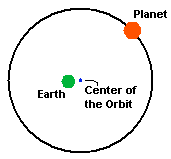 Figure
5. The orbit of the planet is considered eccentric, since
the center of the orbit and the Earth's location are not the same
place. Since the object is not moving at a uniform pace as seen from
the Earth, we would see it changing speed as it went along.
Figure
5. The orbit of the planet is considered eccentric, since
the center of the orbit and the Earth's location are not the same
place. Since the object is not moving at a uniform pace as seen from
the Earth, we would see it changing speed as it went along.
The epicycle and deferent are a way to explain the retrograde motions of the outer planets. The deferent is the large circle that is also eccentric (Earth not in the middle), and upon this large circle, the epicycle is locatd. The planet is found on the epicycle. The planet generally moves in one direction (eastward) most of the time mainly due to the motion of the deferent, except when the epicycle is turned so the planet moves in the opposite direction (westward or retrograde). The entire arrangement is shown in Figure 6.
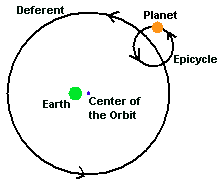 Figure
6. Hipparchus's early model, with the three main aspects all shown
- eccentric, deferent and epicycle. Most of the time the planet moves
in an eastward direction, but on occasion it moves in the opposite
direction (westward).
Figure
6. Hipparchus's early model, with the three main aspects all shown
- eccentric, deferent and epicycle. Most of the time the planet moves
in an eastward direction, but on occasion it moves in the opposite
direction (westward).
All of Hipparchus’s fixes worked pretty good at explaining the general motions of the planets, though they were still not as precise at predicting the motions of the planets - more work needed to be done.

One of the tricky points that Ptolemy tackled was the retrograde motion of the outer planets. He was able to combine several previously proposed devices with some of his own into a system that actually worked. Ptolemy's model was thought to be the best model out there because it produced numbers that were much more accurate than anyone else's. His model used devices such as the the deferent and epicycle of Hipparchus and his own idea, the equant. An equant is sort of like an eccentric, but a bit more off center (this is shown in Figure 7). The planet doesn't move at a uniform rate as measured from the center, but from a point off center. If you were standing at the equant, the motion of the planet would be smooth and uniform - no speed ups or slow downs. If you viewed the motion from any other location, the motion wasn't uniform. The Earth was also off center, so all of this off-centerness really helped Ptolemy in getting the rate of motion correct. Of course, retrograde motion was pretty easy to get into his model by using the epicycles and deferents that Hipparchus introduced.
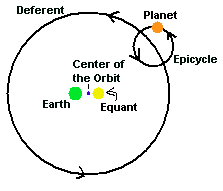 Figure 7.
Ptolemy's model of the sky including the equant. If you watched the
planet's motion from the location of the equant, it would move at a
uniform (steady) rate. Viewing from other locations, like the off
centered Earth, would result in a non uniform motion.
Figure 7.
Ptolemy's model of the sky including the equant. If you watched the
planet's motion from the location of the equant, it would move at a
uniform (steady) rate. Viewing from other locations, like the off
centered Earth, would result in a non uniform motion.
Of course, the worst thing about Ptolemy’s model was that it worked very good at predicting the motions of planets - and he could test his model against all those years of observations in the library, so he could fine tune the parameters in the model. People accepted his model because it worked so well and used all of the basic assumptions (though he sort of fiddled with some stuff - the Earth wasn't exactly in the middle). The details of this model and other observations of Ptolemy are included in his classic work, Almagest. This was pretty much the main textbook of astronomy for many centuries.

Not only were there astronomers in the Arab world, but elsewhere around the world. Astronomers are seen in pretty much every ancient civilization around the world, including the Incas, Aztecs, Native Americans, Pacific Islanders, China, Japan, Korea and so forth. You name it, there were astronomers there. Unfortunately, much of the ancient work of many astronomers has been lost over time - there weren't always convenient places like the library of Alexandria in every country to store this information. Of course, the library at Alexandria wasn't able to survive to the modern era, but was pretty much destroyed in later wars.
As the Europeans started rediscovering the work of Ptolemy and other ancient astronomers through more contact with the Arabic world, they noted that there were problems appearing in Ptolemy's methods. These were in the form of errors in predicted positions which slowly increased in size over the centuries until they were too large to ignore. People didn't want to abandon Ptolemy's model, since it had worked in the past. To make it keep working, they just altered it slightly - usually by adding more epicycles. After a while there were so many epicycles attached it became rather complicated to determine the motion of planets. Perhaps something was wrong with Ptolemy's model?
 Polish
astronomer Nicolaus Copernicus (1473-1543)
Polish
astronomer Nicolaus Copernicus (1473-1543)
Copernicus is the next one on the scene. He was aware of Ptolemy's model, but thought that the increased number of epicycles and the things like the equant were not realistic. He basically scraped the system and produced a heliocentric (Sun centered) model for the solar system. This was a pretty radical concept at the time, but he wasn't completely radical in his model - he also had perfect circles in it and motions that were uniform. Copernicus had to include epicycles to get accurate predictions for planetary motions because of this.
Here's what Copernicus had in his model and how it worked -
1. Put the Sun in the middle.
2. Have everything go around the Sun including not only the Earth but
also all the other planets in the solar system and the stars.
3. By having the other planets go around the Sun, you can easily
explain Mercury's and Venus's motion - they are always near the Sun in
their smaller orbits, so they never get far from it in the sky - they
are visible only in the neighborhood of the Sun either in the early
evening or before sunrise.
4. The motions that we see over the course of the day are due to the
rotation of the Earth on its axis.
5. By having the Earth go around the Sun, we would see the Sun in front
of different constellations over the course of the year. This means the
Sun doesn't have to move!
6. The retrograde motion is easy to explain - this is just what happens
when a faster planet passes up a slower planet. Think of it like this -
if you are on the highway going 65 mph, and there are a bunch of cars
going 60 mph, you would be going past them. Pretend that you are not
moving (you're still going 65 mph, but just ignore the effects of your
motion). If you look at the other cars now, they're going backwards from
your viewpoint. Planets are doing a similar thing so that the Earth
(which is moving faster than Mars) will at times zip ahead of Mars,
making it appear as if Mars is going backwards. (See Figure 8.)
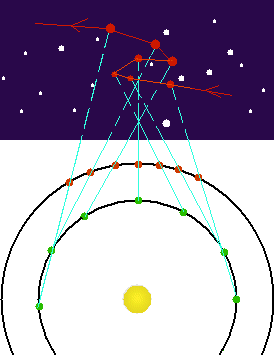 Figure 8.
The retrograde motion of Mars can be explained if we have the Earth
travel around the Sun at a greater speed than Mars. During the time
when the Earth is overtaking Mars, it appears as if Mars is moving
backwards (westward) relative to the background stars.
Figure 8.
The retrograde motion of Mars can be explained if we have the Earth
travel around the Sun at a greater speed than Mars. During the time
when the Earth is overtaking Mars, it appears as if Mars is moving
backwards (westward) relative to the background stars.
7. By having the Earth go around the Sun, you can have the Moon go around the Earth and the phases come about because of this motion. This also easily explains why the sidereal and synodic periods for the Moon are different.
To be perfectly honest, Copernicus wasn't the first person to come up with the idea of having a heliocentric system. A fellow from ancient Greece previously had the idea, but most of his model's characteristics were lost so we don't know exactly what was in his model. You also have to consider the rather curious aspect that Copernicus's model wasn't any better in certain respects than Ptolemy's model. Copernicus did not use an equant but he was still sticking with circles and uniform motions in those circles. This forced Copernicus to have quite a few epicycles to account for all of the motions. This made his model about as complicated as Ptolemy's - different, perhaps even more logical, but not any simpler. The quality of the model wasn't really improved either - you would get about the same accuracy for planetary motions with either Ptolemy's model or Copernicus's so that wasn't much of an improvement.
Copernicus also had to be careful with his model - at least in how
he advertised it or who he spoke to about it. He knew that talking
about a heliocentric model was not only bad philosophically (since it
went against Aristotle) and religiously (since the church preferred a
geocentric model), but promoting a heliocentric model could also be
fatal. You have to remember the time that Copernicus lived in was pretty
volatile. During his life
1517 - Martin Luther posted his theses on the church in Wittenberg,
critical of the Catholic church.
1535 - Thomas More was beheaded for supporting the Pope over Henry VIII
of England.
1536 - John Calvin published "Institutes of the Christian Religion" in
response to persecutions of Protestants in France.
and so on and so on. By the middle of the 16th century there was enough
religious unrest caused by the Reformers, the Counter-Reformers, the
Calvinists, the Protestants, the Lutherans, the Anglicans, the Papists
and everyone else that saying anything contrary to whomever was in
charge was pretty much a guarantee of imprisonment, persecution,
banishment or even a death sentence.
Copernicus didn't really want to promote his theory in part because he worked for the Catholic church and was aware of their position on the Geocentric solar system (they liked it and were against a heliocentric system). He finally did have his theory published (in the book title De Revolutionibus Orbium Coelestium), but he was nearly dead by the time it was printed up. It is interesting to note that in the introduction of the book, which was probably not written by Copernicus, the heliocentric model is described as being only a useful tool in calculating the motion of the planets, and was in no way the real universe - someone was being very careful not to get Copernicus into really deep trouble. Copernicus's book was printed in 1543, the same year he died and by 1616, the book was placed on the Prohibited Books list by the Catholic Church.
Sort of to press home the point as to how serious some people were about these things, just see what happened to the philosopher Giordano Bruno (1548-1600). He supported Copernicus's model and also went so far as to say that the stars were infinite and there were infinite worlds beyond our own. Though it isn't entirely clear why he was arrested and imprisoned by the Inquisition, it is a fact that he was burned at the stake in 1600. He must have really made someone very, very mad!

Tycho's observations and discoveries about the "nova" got him on the very good side of the King of Denmark; so good, in fact, that the King gave him an island to build an observatory, a workshop and labs on. The observatory and its instruments were built for precise work and that is what Tycho is known for - his accurate observations of the night sky. He had made excellent observations of everything including not only the stars but also a comet and the planets' positions. His observations of the comet gave him the same result as he got for the "nova," that the comet was so far away it did not show a parallax. It looks like this is an example of how the sky was not as the ancient Greeks thought - things did change. His observations of the comet were important since people at that time thought comets were close to the Earth - they usually assumed them to be objects in the atmosphere. This idea was due to the fact that comets moved relatively quickly compared to other things in the sky and they were something that changed in appearance. Since Tycho's observations did not show a parallax, he proved that the comet must be really far away, not an object in the atmosphere but well beyond the distance to the Moon.
Tycho had years of very precise observations of the motions of the planets. How was he able to do this? He didn't use a telescope; all observations were made with his unaided eye. He just did the same observations over and over and over and over... By repeating the observation, you reduce the amount of inaccuracy. This is what Tycho did.
Eventually Tycho's luck ran out. The King that favored him died, and the next King didn't really like Tycho, so he got out of Denmark and went to work for the Holy Roman Emperor in Prague (of course the Holy Roman Emperor was neither holy, nor a Roman nor an emperor, but I digress). While there he hired a number cruncher to do some calculations - Tycho didn't really like to do the math; he preferred to do the observations - sort of like how some astronomers are today; some stay at the telescope all the time, and some sit in front of a computer all the time. Tycho was trying to come up with a model of the solar system that was actually a bit of a hybrid between Copernicus's and Ptolemy's, but he didn't want to do the math. Tycho's career in Prague was sort of cut short when Tycho partied just a little too much one night and died (1601).
 Johannes Kepler
(1571-1630)
Johannes Kepler
(1571-1630)
Kepler was the poor fellow who Tycho hired to do all of the messy calculations. But when Tycho died Kepler had access to all of his data. This is really what Kepler wanted all along. Kepler was fairly obsessed with figuring out the motions of the planets. And he knew that to do that, and to do it right, he needed the best data. Tycho’s death gave him that data.
Kepler liked the model that Copernicus came up with, but he couldn't get it to work using only those dang circles. Over time he finally did hit upon the correct solution and gradually came up with the Three Laws of Planetary Motion. It should be noted that these laws do not explain WHY the planets move, but they just show HOW the planets move. He wasn't able to figure out what the force was that drove the planets in their paths, but at least he had a way of figuring out how to accurately determine their locations - much more accurately than Ptolemy's or Copernicus's models ever could. It took many years for Kepler to derive each law, and of course he had different names for them (he didn't call them Law #1, #2 and #3 like we do now). Without much further ado - here are the three laws of planetary motion...
1. Planets move in ellipses with the Sun at one focus. (See Figure 9) There are several aspects that can be explained by using an ellipse and not a circle to explain the planetary motions. By using an ellipse, the planet can be closer or further from the Sun since the Sun is not in the middle, and the ellipse stretches out the orbit. Where is the Sun? The Sun is close to the center but it is not in the center. It is actually found in the location known as the focus (plural: foci). This is a position in an ellipse that has mathematical meaning which we'll get to. For the most part, the planets in the solar system have orbits that look to be very circular, but are actually elliptical. The elliptical aspect is not easy to see for the most part but it is there. By using an ellipse, Kepler could get rid of the things that Ptolemy and Copernicus used (stuff like deferents and epicycles) to make the numbers come out right.
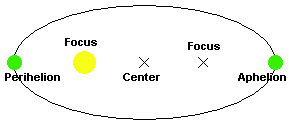 Figure 9.
Basic aspects of an ellipse showing the Sun's location (at a focus),
and the two points where the Earth is closest and furthest from the
Sun.
Figure 9.
Basic aspects of an ellipse showing the Sun's location (at a focus),
and the two points where the Earth is closest and furthest from the
Sun.
There are times when a planet is closest and furthest from the Sun, because the planets orbit in ellipses. Aphelion is when it is furthest from the Sun and perihelion is when it is closest to the Sun. The distance between the Earth and the Sun is always changing. If that is the case, how can you answer a question like "How far is the Sun from the Earth"? We do that by using a very convenient average of the distance between the Earth and Sun. The average is 150 million km. That's not convenient! How's this - the average distance between the Earth and the Sun is 1. Yes, it is 1 Astronomical Unit (or abbreviated as 1 A. U.). This is sort of like avoiding the use of small units of distance to measure large distances. You could say that you were 66 inches tall. Is that tall? If you remember that there are 12 inches in a foot, and use feet instead of inches as your unit of measure, 66 inches is the same as five and a half feet. You could go around saying that the average distance between the Earth and the Sun is 150 million km, or you could say it is 1 A.U. Which is easier? Well, duh, the A. U. is easier to use. The A.U. is also a handy distance for other objects in the solar system; you could say that Mars is 1.5 A.U. from the Sun, or that Jupiter is a bit more than 5 A.U. from the Sun. By giving the distances in A.U., you have their distances scaled to the Earth's distance (Mars is 1.5x further from the Sun than the Earth, while Jupiter is a bit more than 5x further from the Sun). This a lot easier to comprehend then to say Mars is 223 million km and Jupiter is 778 million km from the Sun, right?
Now to answer the question, what actually are the foci? They are a way that ellipses are defined - the distance from one foci to the edge of the ellipse and over to the other foci is always the same - see Figure 10 for this. Now here is a rather nifty thing - a circle is actually a type of an ellipse. In this case, both foci are located in the center.
 Figure 10. The
foci-edge-foci distance remains constant - so that all of the
different colored line segments have the same total length.
Figure 10. The
foci-edge-foci distance remains constant - so that all of the
different colored line segments have the same total length.
To distinguish between the different types of ellipses, a value known as the eccentricity is used. The value of the eccentricity is defined as the ratio between the distance between the foci divided by the longest distance across the ellipse. These are shown in Figure 11. As the ellipse gets more stretched out, the eccentricity gets larger.
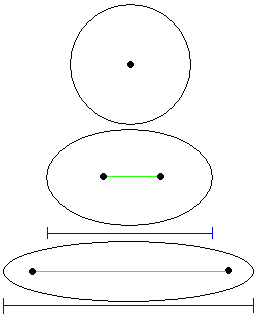 Figure 11.
The eccentricity would be the value of the foci-foci distance (green
line) divided by the widest part of the ellipse (blue line). For the
circle, the green line has a value of 0, so the eccentricity for a
circle is 0. For the other two ellipses, the eccentricity increases as
the foci get further apart.
Figure 11.
The eccentricity would be the value of the foci-foci distance (green
line) divided by the widest part of the ellipse (blue line). For the
circle, the green line has a value of 0, so the eccentricity for a
circle is 0. For the other two ellipses, the eccentricity increases as
the foci get further apart.
Time for the second law -
2. A planet moves faster at perihelion than at aphelion. Sometimes this law is stated as "equal areas swept out in equal times," which is not the most straightforward definition in the world. See Figure 12. This law basically says that when a planet is closer to the Sun (at perihelion), it is moving faster in its orbit about the Sun than when it is far from the Sun (at aphelion). The Earth moves around the Sun fastest when it is closest to it (this occurs in early January). Kepler originally derived this law using wedges and triangles to measure the areas so the old phrase with "equal area" is often quoted, though it is a bit confusing. If the ellipse is very close to being a circle, there is little variation in the speed. As long as it is an ellipse, the speed difference is there. If the orbit is very elliptical (stretched out), then the difference in aphelion and perihelion speeds are great.
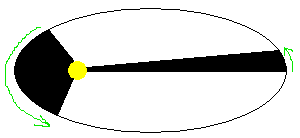 Figure 12.
Kepler's Second Law - planets travel
faster in their orbits when they are near the Sun, and slower when they
are away from the Sun. If the motion of a planet for one month is shown
(the planet moves the distance designated by the green arrow) then the
planet nearer the Sun is obviously moving faster. If you could measure
the area created by a planet as it moves in its orbit during one month,
the area would always be the same size (the two black wedges have the
same size so long as they were created during the same time span).
Figure 12.
Kepler's Second Law - planets travel
faster in their orbits when they are near the Sun, and slower when they
are away from the Sun. If the motion of a planet for one month is shown
(the planet moves the distance designated by the green arrow) then the
planet nearer the Sun is obviously moving faster. If you could measure
the area created by a planet as it moves in its orbit during one month,
the area would always be the same size (the two black wedges have the
same size so long as they were created during the same time span).
Last but not least, the third law, and this one is a formula -
3. If you define the period of the orbit as P and the average distance from the Sun as a then you get the following relation -
P2 = k a3
What's k? That is a constant (a non-changing number) for the situation you are looking at. The basic upshot of this formula is, the more distant planets (big a values) take longer to go around the Sun (big P values). Average distance is used in the formula (remember a is the average distance), since the distance between the planet and the Sun is always changing (Law #2). As P increases, so does a, and as P decreases, so does a. You could say it the other way (as a increases, so does P ...).
One of the neat things about Kepler's laws is that they can be used for anything orbiting anything else - not just planets going around the Sun, but also for moons or satellites going around planets, stars going around the galaxy, or entire galaxies going around one another. We'll see this later. The trick, though, is to use the correct value of k. The value of k will depend upon what the orbiter and orbitee are - the value for k will vary from one system to the next, so you will need to know it before you can use the formula. You could find it if you know what P and a are.
There is also a special situation that makes using the law
really convenient. If P is measured in years, a is
measured in A.U.s and the object is orbiting the Sun then the
following statement applies (in this case k=1) -
P2 = a3
For the Earth we have P=1, a=1, so we get 1=1. I suppose you don't believe me. Let's try another planet. For Mars P=1.88, which when you square it P2=3.52. What would a be in this case? a3 has to equal 3.52, so by taking the cube root of 3.52 you get a, which in this case ends up being 1.52 - and this is the correct value for a (you can verify all of this by looking up the value for P and a somewhere for any of the planets in our solar system).
Here's another example: What would the period of a planet be if its average distance from the Sun is 4 A. U.? You have a value for a, and you need to get P. You can use the special short version of the formula, since you are orbiting the Sun. Now you need to calculate a3 = 4x4x4 = 64. This means that P2= 64. What times itself is 64? P must be 8 (since when you square it you get 64). It would take eight years for an object to orbit the Sun if it has an average distance of 4 A. U.
What if the orbit is very elliptical, how can you determine the value of a? Actually it is quite easy. By definition, a is 1/2 the longest width in an ellipse - in Figure 11, a would be 1/2 the length of the blue line. Take a peak at the ellipses in Figure 13. An object orbiting along those paths would take the same amount of time to complete one orbit, since they all have the same length for their longest axes.
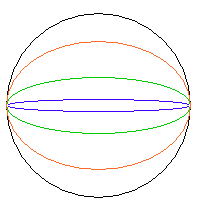 Figure
13. Different eccentricity ellipses all with the same length for
their long axis (so also the same value for "a" for each of them).
Planets traveling in these orbits will all take the same amount of
time to complete one orbit.
Figure
13. Different eccentricity ellipses all with the same length for
their long axis (so also the same value for "a" for each of them).
Planets traveling in these orbits will all take the same amount of
time to complete one orbit.
I should mention the fact that laws 2 and 3 deal with distances, but not in the same way. Law 2 deals with how the changing distance of a planet in its orbit affects its speed in orbit, while Law 3 deals with an average distance and how that relates to the time for one orbit. Don't get these two mixed up. For example, looking back at Figure 13 with the different eccentricity ellipses - the most circular one would have the most uniform speed - little change in velocity at any point in a planet's orbit, while the most eccentric one would have a wide range in velocity, from very fast at perihelion to very slow at aphelion. In spite of these speed differences, since all the ellipses have the same width, an object would take the same amount of time to travel around the Sun regardless of which of these paths it was on.
With his 3 laws (which took him years to figure out), Kepler was able to calculate the orbits of the planets very precisely, much more precisely than could be calculated using Ptolemy's or Copernicus's models. Again, it should be noted that Kepler really didn't know why his laws worked; he did not know what the force was that was behind the motions. He actually was sort of favoring some kind of cosmic magnetism, but that's not right.
Again, it should be emphasized that while Kepler came up with his laws so that he could explain the complex motions of the planets, his laws apply to anything orbiting anything else. So the Moon orbiting the Earth obeys Kepler's Laws, and a distant star orbiting another star obeys Kepler's Laws - it's not just for planets!
 Galileo
(1564-1642), who was born in Pisa Italy.
Galileo
(1564-1642), who was born in Pisa Italy.
While Kepler's ideas were pretty much banned by the Church (that was both a religious thing and a political thing) someone found his ideas very interesting, as well as Copernicus's theories. That fellow was Galileo, a rather outspoken gentleman who did a lot of work in physics trying to figure out how things moved. His main contributions to astronomy were not his theories of how the planets moved but his use of the telescope. He did not invent the telescope (someone in Holland did that), but he learned about the invention, improved upon it and made one that was much better than the original design. The telescope was originally used by sailors to view great distances over the water to spot other ships and land. Galileo used his telescope to look at the sky. In just a few short weeks his observations of the sky literally blew his mind and gave him evidence that convinced him that Copernicus (and Kepler) were right. What did he see? (If you click on the items below, you'll see the drawings that Galileo made of his observations.)
The Moon was a place like Earth with
mountains, valleys, and other features that also exist on the Earth. It
was not a perfect heavenly object. Remember, things in the sky were
supposed to be perfect and eternal - and with all the bumps, holes and
rough surface features visible on the Moon, Galileo could see that it
was far from perfect.
The Moon does not generate its own light, but is bright due to light
that it reflects from the Sun. This is obvious from the way that the
shadows are cast on the Moon by the ridges and mountains there.
Venus goes through phases like the Moon. This is easy to explain if it orbits the Sun. If it orbited the Earth, as in Ptolemy's model, then it would not have the range of phases that Galileo saw. Galileo could also see that Venus's size changed along with its phases, indicating that it was getting closer or further away from the Earth - how could it do that if the Earth is in the middle and Venus is on a perfectly circular orbit around it? Frankly, it can't, because the Earth is not in the middle and Venus is not in orbit about the Earth. (See Figure 14).
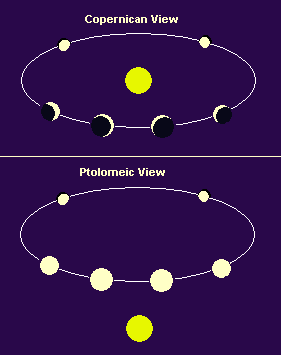 Figure
14. Two ways that Venus and the Sun could be viewed from the Earth.
In the geocentric view (bottom), the Sun and Venus must orbit the
Earth. In that case, Venus would always be located so that most of its
lit surface would be visible from the Earth. This is not what Galileo
saw. His observations confirmed the Copernican view - that Venus orbits
the Sun (as does the Earth). In this case we would see Venus go through
a variety of phases and it would increase and decrease in size as it
orbited the Sun.
Figure
14. Two ways that Venus and the Sun could be viewed from the Earth.
In the geocentric view (bottom), the Sun and Venus must orbit the
Earth. In that case, Venus would always be located so that most of its
lit surface would be visible from the Earth. This is not what Galileo
saw. His observations confirmed the Copernican view - that Venus orbits
the Sun (as does the Earth). In this case we would see Venus go through
a variety of phases and it would increase and decrease in size as it
orbited the Sun.
There are four objects orbiting Jupiter.This broke the old rule "everything orbits the Earth." How's this possible? Galileo tried to make some money by naming the four objects the Medici Stars, but we all know them today as the Galilean satellites (the Medicis were the folks that ruled most of central Italy - sort of like the most powerful multinational corporation of their day, but quite a bit more ruthless). If these things don't orbit the Earth, then how can they exist in Ptolemy's or Aristotle's models? They can't. They are okay in Kepler's model. In fact, if you watch the little "stars" move around Jupiter, you can determine that they obey Kepler's laws of motion (those further away from Jupiter have longer orbital periods).
There are things on either side of Saturn that sort of look like "ears". This breaks the rule about everything being a perfect circle in the sky. Galileo's telescope was good, but not good enough for him to see the rings of Saturn clearly.
Then Galileo did a big time stupid thing, he pointed his telescope at the Sun. While he was damaging his eyes he noted that there were "blemishes" on the Sun (what we call sunspots). This is another instance of imperfections in the heavens. Of course, doing something as stupid as pointing his telescope at the Sun contributed to the blindness that he had later in life.
Galileo's ego got him into a lot of trouble with the church. He published quite a few books about his theories and observations but the one that really got him in trouble was his book Dialogue concerning the Two Chief World Systems, published in Florence in February 1632. It probably wasn't so much about what he said in Dialogue, but how he said it. The book was basically a debate between three people, one supporting Ptolemy and Aristotle, one supporting the Copernican view and one who was on the fence. The person supporting Aristotle's view is named "Simplicio," and he's portrayed as a fool. Some people thought that the character of Simplicio was an amalgamation of a bunch of different people, mainly scientists and church officials who held on firmly to the Aristotelian view. I guess some people just don't respond too well to criticism. Unfortunately for Galileo, these were people you do not want to offend! He was put on trial and forced to recant all that he taught about the heliocentric model. Galileo had to spend the rest of his life under house arrest. He eventually went blind and died in 1642.

In order to understand how the Universe work, Newton had to set up some ground rules that pretty much are the basis for all kinds of motion in the Universe - not just motions of planets, but motions of everything. These are his Three Laws of Motion.
Law #1. Stated very simply "An object at rest stays at rest, and a body in motion stays in motion. This situation can be changed if the object is messed around with by something." Okay, so the original statement of this law did not say "messed around with," but I think you understand what I mean. Stuff will keep doing what it is currently doing if no one or nothing messes around with it. A pencil will stay laying on a table for all eternity so long as nothing touches it (and the table lasts forever). If an object rolls across the floor it will keep rolling forever. Wait a minute - that's not correct. If you roll a ball down the hall it will eventually stop. It stops because something messes with it, in this case, the friction of the floor. If there was no friction, no resistance to the motion, then the ball would go down the hallway forever.
You may have heard this law called the Law of Inertia. Another thing about this law is what the motion is like. The motion should be straight, assuming that the surface is straight. An object should always move in a straight line at a steady speed unless something alters its motion. You may have experienced this effect in a roller coaster or a car, depending upon how fast you drive. If you are in a roller coaster and it is going straight, everything is fine. Then the track curves to the side, and fortunately the roller coaster car stays on the track and goes around the curve - what happens to you? Your body wants to keep going forward - things want to do what they are currently doing - but the car has changed direction. This results in you getting thrown to the side of the car. Actually, another way of looking at this is that the car is the one that ran into you; after all, you were going along just fine when it decided to change direction. A change in direction is another way of looking at motion changing.
Law #2. This one is pretty much a definition. If m=mass (material, stuff) and a=acceleration (a change in motion) then
More mass requires a greater force to accelerate it (get it moving,
slow it down, or change the direction of the motion). It is harder to
get a locomotive moving than it is to get a Volkswagen moving. You could
also look at how the different masses act under the influence of the
same force. Let's say you have a baseball bat and you hit two objects,
a baseball and a bowling ball. What sort of motion results? If you said
that the baseball will move further than the bowling ball, then you
were right. You could solve this numerically. Let's say that the
bowling ball has 100 times more mass (m)
than the baseball (I really have no idea; I don't bowl). How do their
accelerations compare? The baseball will be accelerated 100 times more
than the bowling ball. If the force applied to both is the same (same F), then the values relating the m and a should be equal in size but
opposite in their sense (m big, a small and m small, a big).
In case you were wondering, mass is NOT weight. Mass is the measure of the amount of stuff in objects. Weight is just how much pull you feel due to the gravitational acceleration of the Earth. So weight is caused by the acceleration of gravity due to your location and circumstances, and it can change with location and/or circumstances, while your mass doesn't change (unless you eat too much/little). Don't you feel like you weigh more when an elevator is starting to go up? It is accelerating, and unless you are eating a donut, your mass isn't changing, yet you feel heavier - you are feeling a new force along with the regular force of gravity. The Earth is constantly accelerating (pulling) you downward. We'll get to that. That's why you always fall down rather than up.
Law #3. "For every action there is an equal and opposite
reaction." You've probably heard this one before. You might want to
think of it as the "you can't get away with anything" law. If you do
something, you will get something done back at you. If you hit your
hand against the table, the table hits back at you - that's why it
hurts, so don't do it! If you keep hitting the table, you might want to
note how you are hitting it - you're exerting a downward force, while
the table is exerting an upward force on you - that's the "opposite"
part of the rule. While you might not think that the law is "equal"
since your hand hurts and the table doesn't appear to be damaged -
don't worry, it is getting hurt. Just keep hitting it for about five
hours - you'll eventually see some effect of the force that you are
exerting, though of course your hand will be pretty much ruined by this
time.
While these rules might not seem all that Earth shattering, they are.
They are just the basis for all the motions of the Universe. To actually
figure out what was driving these motions, Newton had to use these laws
and the concepts behind Kepler's laws to formulate a rule that could
explain the motions of all objects in the Universe.
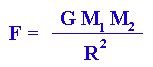
F=Force of Gravity, you may want to think about this as the
amount of "pull" something has
G=Constant - don't worry about what it is, you usually won't
have to know it to use this formula.
M1, M2 = masses of the objects, you need
two to tango and two masses are also needed for gravity.
R = the distance between the center of masses of the two
objects. We'll simplify this, since most important things in astronomy
are fairly spherical, so R can be thought of as the distance
between the two objects’ centers.
Just remember, if you change the masses or the separation then the force of gravity changes. Let's try an example. Let's say you travel to a distant planet called Gumbyville. This planet has a mass that is four times the mass of the Earth. How does its gravity compare to the Earth's? The only difference from the Earth's gravity is an extra factor of four in the top of the formula. You would feel a force of gravity that is four times what you feel on the Earth - you would weigh four times what you weigh now. Let's suppose that this planet also has a different radius than the Earth. The planet's radius is three times that of the Earth. Now here's where most people mess up - the distance value, R, has a two next to it, indicating that it should be squared. If you change the value of R, then the change gets squared as well. For Gumbyville, this results in a value of 3x3=9 on the bottom of the formula. What does that give us? A four on the top and a nine on the bottom - the overall effect is that the force of gravity is 4/9 that of the Earth, or slightly less than 1/2. You would actually weigh less even though Gumbyville has more mass than the Earth.
Here's something you don't want to forget - Gravity is the most important force in the Universe! Yes, it is even more important than Obi-wan Kenobi and the Force! Gravity doesn't go away; it is always there pulling things together or squeezing things down. It is always ready to take over a situation if you give it half a chance. As you'll see, without gravity there would be no galaxy, Sun or Earth - it pretty much is the main driving force behind the whole Universe.
Using the formula for gravity that he came up with and some basic calculus, Newton was able to redo Kepler's laws and explain the motions of the planets as an effect of the force of gravity. A couple of things can be seen in how Kepler's laws behave if you look at them in terms of gravity - like the second law, which says that planets move faster in their orbits when they are closer to the Sun. If they're closer to the Sun, what's the gravity like? The gravity must be stronger since the distance is smaller, so the planets are feeling more of a pull from the Sun (and of course the Sun feels the pull from the planets, but it's so big it doesn't really care). How can the planet prevent itself from being pulled into the Sun due to the increasing pull of gravity? If it goes faster in its orbit, it will be able to balance out the force of gravity - sort of like having to swing a bucket full of water around fast enough to prevent any of the water from falling out. Further from the Sun there is less of a pull and the planets don't have to move as fast. You have to remember, Newton's laws and even Kepler's laws are not confined to just planets; they can work all over the Universe on all sorts of objects including the Universe itself.
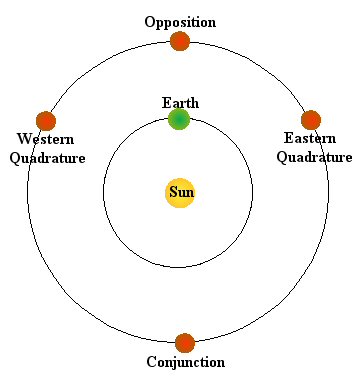 Figure 15. The main named locations for the
Superior Planets.
Figure 15. The main named locations for the
Superior Planets.
The positions are sort of similar to the Moon's various locations.
For example, the opposition
location is like the Full Moon; a planet there would be visible high
overhead at Midnight, it would rise around 6 PM and set around 6 AM.
The quadrature locations are
sort of like the quarter phases of the Moon, at least in terms of the
questions of "when do they rise," "when do they set," etc. This is
because quadrature and the quarter phases of the Moon both are
positions when the object is 90 degrees away from the Sun. The two
quadratures are distinguished as being eastern quadrature
or western quadrature if the object is 90 degrees east
or 90 degrees west of the Sun respectively. Of course,
the location designated as conjunction
would be most like the New Moon, but in this case the planet is behind
the Sun, not in front of it. A planet at conjunction would be doing
things at the same times as the New Moon or the Sun does them (rises at
sunrise and sets at sunset).
Inferior Planets are those located inside of the Earth's orbit and include Venus and Mercury. Their main alignments are shown in Figure 16.
The position of conjunction depends upon whether the planet is in front of (inferior conjunction) or behind (superior conjunction) the Sun. As with the superior planets, a conjunction is an alignment in the direction of the Sun. The other two positions indicate when the planet is at its greatest angular distance from the Sun. If it is west of the Sun as far as it can get (from our perspective), it is at maximum western elongation, while being east of the Sun puts it at maximum eastern elongation. Sometimes the phrases greatest eastern elongation and greatest western elongation are used - either way it means the same thing. These planets are always seen near the Sun and are really only visible when the Sun is out of the way, so either before the Sun has risen or after the Sun has set. When a planet is to the East of the Sun, it would be visible in the Evening sky after the Sun sets (you can remember this by noting both begin with "E" - east, evening). A planet located to the West of the Sun would be visible in the Morning sky before the Sun rises (you can remember this by thinking of the M as an upside down W).
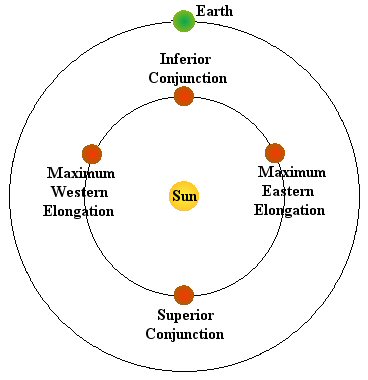 Figure 16. The main named locations for the
Inferior Planets.
Figure 16. The main named locations for the
Inferior Planets.